Table of Contents
Properties of Whole Number
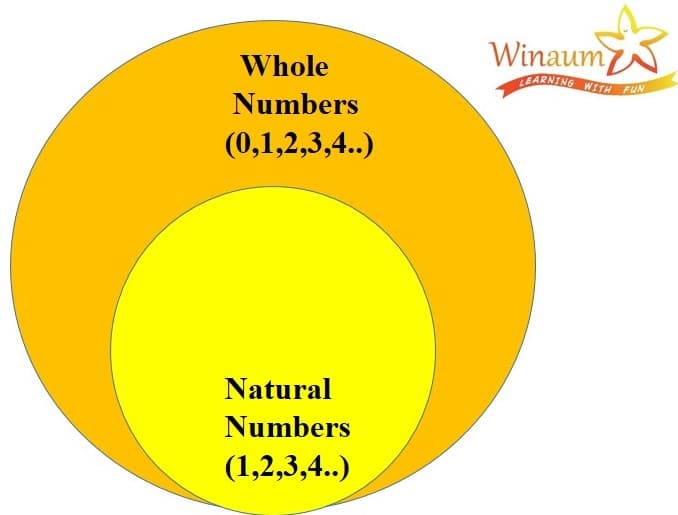
To understand the concept of Whole Numbers first we need to know what are Natural Numbers and then we will be able to understand about Properties of Whole Number.
Natural Numbers come naturally when we start counting like numbers 1,2,3,4 and hence they are called Natural Numbers.
Introduction
Whole Numbers are the natural numbers along with ‘ 0’. Therefore the numbers 0, 1,2,3,4,5 are called Whole Numbers.
Before knowing the Properties of Whole Numbers we should understand the following:-
- The successor of a Whole Number
- The predecessor of a Whole Number
- Representation of Whole Numbers on a Number Line
The properties of Whole Number are better understood with respect to the different operations in maths for addition, subtraction, multiplication, and division. It helps in many problems in an easier manner with the use of these properties.
At Winaum Learning, we believe that maths is a science that deals with logic, shapes, numbers, patterns, and arrangement. It is a life skill and requires an in-depth understanding. Students at Winaum Learning Maths Program do maths with worksheets, practice tests, continuous revisions of the concepts, activities, and games.
Closure Property
1. Closure Property in Addition :
If a and b are two whole numbers then a+b is also a whole number.
Example 1 : a= 4, b=7
then 4+7 = 11 , implying 4, 7, and 11 all are whole numbers.
Example 2 . a = 4, b = 6, a + b = 10
Now a and b are whole numbers, hence the result of addtition of a+b is also a whole number.
Therefore 4 + 6 = 10 , 10 is also a whole number.
Example 3. Suppose a = 5, b = 9,
Then a + b = 14
5 + 9 = 14
Implying a+b which equals 14 is also a whole number.
Example 4. If a = 8, b = 3, and a &b are whole numbers, then
a + b = 8 + 3 = 11
11 is also a whole number.
- a = 6, b = 10, a + b = 16
6 + 10 = 16
To summarise: On the Addition of any two whole numbers, you will see that the result of addition is again a whole number.
2. Closure Property Multiplication:
If a and b are two whole numbers then a x b is also a whole number.
Example 1. If 4 and 7 are whole numbers then,
4 x 7 =28.
Implying 4, 7, and 28 all are whole numbers.
Example 2. Asssume a and b are whole numbers and if a = 3, b = 6,
=> a x b
=> 3 x 6 = 18
Implying 3, 6, and 18 all are whole numbers.
Example 3 . If a = 5, b = 11, and a &b are whole numbers, then
=> a x b
=> 5 x 11
=> 55
Implying that 5, 11, and the multiplication result 55 all are whole numbers.
Example 4. If a = 9, b = 2, and a & b are whole numbers, then
=> a x b
=> 9 x 2
=> 18
Implying that 9, 2, and the multiplication result 18 all are whole numbers.
Example 5. If a = 1, b = 8, and a &b are whole numbers, then
=>a x b
=>1 x 8 = 8
Implying that 1, 8, and the multiplication result 8 all are whole numbers.
To Summarise: As we look at the examples above when we multiply any two whole numbers, then you will see that the multiplication result is again a whole number.
To understand the Properties of Whole Number and other topics related to enhancing maths understanding, Winaum Learning offers Online, Live, Interactive Classes in small batches to kids in order to develop their strong mathematical foundation. Book a Free Class Today.
Commutative Property
Commutative Property in Addition
If a and b are two whole numbers, then
a + b = b + a
If we change the order, the sum of whole numbers remains unchanged.
The sum of two whole numbers remains the same even after interchanging the order of the numbers.
- Example 1
If a and b are two whole numbers and a = 5, b = 5,
Then as per this property a + b = b + a
5 + 5 = 5 + 5
10 = 10
So if we see above the answer on the left-hand side and the answer on the right-hand side, both answers are 10.
- Example 2: If a and b are two whole numbers and a = 7, b = 8.
Then as per this property a + b = b + a
7 + 8 = 8 + 7
15 = 15
So if we see above the answer on the left-hand side and the answer on the right-hand side, both answers are 15.
- Example 3 :
If a and b are two whole numbers and a = 3, b = 9.
Then as per this property a + b = b + a
a = 3, b = 9,
a + b = b + a
3 + 9 = 9 + 3
12 = 12
So if we see above the answer on the left-hand side and the answer on the right-hand side, both answers are 12.
- Example 4. If a and b are two whole numbers and a = 6, b = 8.
Then as per this property a + b = b + a
a = 6, b = 8
a + b = b + a
6 + 8 = 8 + 6
14 = 14
So if we see above the answer on the left-hand side and the answer on the right-hand side, both answers are 14.
- Example 5. If a and b are two whole numbers and a = 7, b = 5,
a + b = b + a =12
7 + 5 = 7 + 5
12 = 12
So if we see above the answer on the left-hand side and the answer on the right-hand side, both answers are 12.
Commutative Property in Multiplication
For any two whole numbers a and b
a x b =b x a
This implies that the product of whole numbers remain unchanged even if change the order of numbers while multiplication.
6 x 12= 12x 6
72= 72
Here at Winaum Learning, the Commutative properties of addition and multiplication and other Properties of Whole Number are well understood by the students with maths exercises, assessments, puzzles, and math activities at Winaum Learning online maths classes. Book a Free Trial.
Associative Property
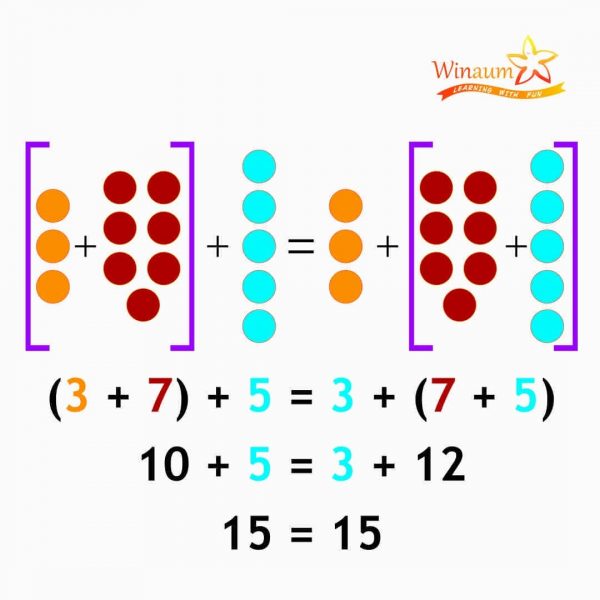
Associative Property of Addition
If a, b, and c are three whole numbers then ( a+b ) + c = a+ ( b+c ). This implies even if we change the association of numbers, the result does not change.
For Example: a= 3, b=7, and c= 5, then
3+7+5= 3+(7+5)
10+5= 3+12
15=15
LHS= RHS
Even if the grouping of the numbers has changed both on the left-hand side and the right-hand side, the result does not change, it’s 15 on both sides.
Associative Property of Multiplication
If a, b, and c are three whole numbers then
( ax b ) x c = ax ( b x c ). This implies even if we change the association of numbers , the result does not changes.
Identity Element
The identity element of addition for whole numbers is 0 i.e on adding 0, the number shall remain unchanged. It implies that the sum of any whole number and zero ( 0 ) is the number itself.
General Property: a+0 = a
- Example 1 : Assume a= 17, then 17 + 0 = 7 ( i.e. number itself )
- Example 2 : Assume a = 125, then 125 + 0 = 125 ( i.e. number itself )
Distributive Property of Multiplication
Distributive Property in Addition
The Distributive Property says that when we multiply the sum of two or more addends by a number, then it will give same answer as multiplying each addend individually by the number and then adding each of the multiplication results.
General Property: a × ( b + c ) = ( a × b ) + ( b × c )
Example 1: Let a = 3 , b= 5 and c = 8
3×( 5+8 ) = (3× 5)+(3×8)
3 × 13 = 15 + 24
39 = 39
LHS = RHS
Example 2 : Let a = 10, b = 7 and c = 12
10×(7+12)=(10×7)+(10×12)
10 × 19 = 70 + 120
190 = 190
LHS = RHS
Example 3 : Let a = 25, b = 11 and c = 40
25×(11+40) =(25×11)+(25×40)
25 × 51 = 275 + 1000
1275 = 1275
LHS = RHS
Example 4 : Let a = 100, b = 70 and c = 30
100×(70+30)=(100×70)+(100×30)
100 × 100 = 7000 + 3000
10000 = 10000
LHS = RHS
2. Distributive Property in Subtraction
According to distributive property multiplying the difference of two numbers by a number will give the same result as multiplying each number individually and then finding the difference of the products.
General Property: a × (b – c) = ( a × b )– ( a × c )
Example 1: Let a = 9 , b = 5 and c = 2
9×(5–2) = (9×5)– (9×2)
9 × 3 = 45 – 18
27 = 27
LHS = RHS
- Example 2. Let a = 11, b = 10 and c = 7
11 ×(10–7) = (11×10)–(11×7)
11 × 3 = 110 –77
33 = 33
LHS = RHS
- Example 3 : Let a = 50, b = 25 and c = 12
50×(25–12)=(50×25)–(50×12)
50 × 13 = 1250 – 600
650 = 650
LHS = RHS
- Example 4 : Let a = 100, b= 75 and c = 20
100×(75–20)=(100×75)–(100×20)
100 × 55 = 7500 – 2000
5500 = 5500
LHS = RHS
Here at Winaum Learning, the Distributive Property of Multiplication with addition and subtraction and other Properties of Whole Number are well understood by the students in an active learning environment with maths orals, written work, exercises, assessments, puzzles, and other math activities at Winaum Learning online maths classes. Book a Free Trial.
Difference Between Counting Numbers and Whole Numbers | ||
S.No | Counting Numbers | Whole Numbers |
1 | Natural numbers are defined as the basic counting numbers. The counting number or natural number are {1, 2, 3, 4, 5, …}. | Whole numbers are defined as the set of natural numbers, and it started with zero. The whole numbers are{0,1, 2, 3, 4, 5, …}. |
2 | Counting or Natural Numbers are represented using the letter “N”. | To represent Whole Numbers we use the letter “W”. |
3 | Counting number starts from 1. | Whole number starts from 0. |
4 | We can say that all the counting numbers are considered as whole numbers. | All the whole numbers are not considered as counting numbers as 0 is not a counting number. |
Conclusion
To summarise there are 5 Properties of Whole Number that are Closure Property, Commutative Property, Associative Property, Identity Element and Distributive Property. Above we have gone into details understanding of the concept by giving several examples for each property.
Frequently Asked Questions on Whole Numbers
Whole numbers are the positive numbers starting from the number 0 and go up to infinity.
For children at an early age, it is easiest for them to understand whole numbers as they can do counting comfortably with it. The four main pillars of Mathematics -addition, subtraction, multiplication, and division can be understood well when the foundation of numbers and counting is clear to the kids.
Zero – “0” is the smallest number whole number.
All the numbers starting from 0 like 0,1,2,3 4,5… are whole numbers as they are not decimals or fractions.
- Whole numbers is a set of positive integers.
- 0 is also a whole number.
- All the whole numbers except 0 are natural numbers too.
Numbers that are negative, fractional numbers having denominators other than 1, and irrational numbers are the numbers that are not whole numbers.
No, whole numbers can’t be negative. In fact, it is a set of positive integers.
Yes, all the natural numbers are whole numbers.
Yes, all the whole numbers are real numbers.
External Links
Related Pages on Numbers
About Winaum Learning
Winaum Learning offers an educational platform for kids for developing their skills in Maths via (Curriculum program-Grow with Maths and Vedic Maths ), Handwriting, and English grammar. It offers kids online live classes and offline sessions done in small batches through its trained and expert teachers. It organizes competitions also for maths-IMC and handwriting- IHC. Know more by signing up for a trial class.